modulation matrix

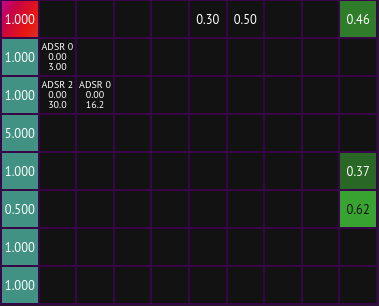
The modulation matrix is the interface that controls each of the [operator]s in the [fm-synth]. It allows the [modulation-index] for each [operator] in the FM synth to be provided, and also provides configuration for each of the operators themselves and their output levels.

The [fm-synth] has 8 [operator]s, which are the components of the modulation matrix. Each operator optionally modulates each of the other 7 operators as well as itself via feedback. Each cell of the main body of the modulation matrix controls how much each operator modulates one of the others (or itself).

operator configuration

The left-most column of the modulation matrix contains configuration for each of the 8 [operator]s. The number displayed in each one corresponds to the base frequency multiplier that is used to determine the frequency at which each operator oscillates.

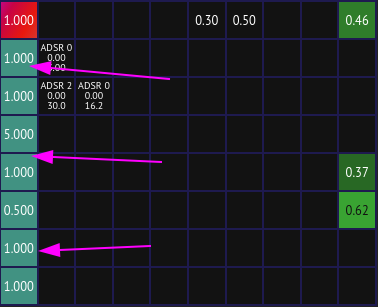
To change this value and configure other parameters about the operator, click its cell. This will highlight the cell in red and open up the operator configuration screen to the right of the modulation matrix:

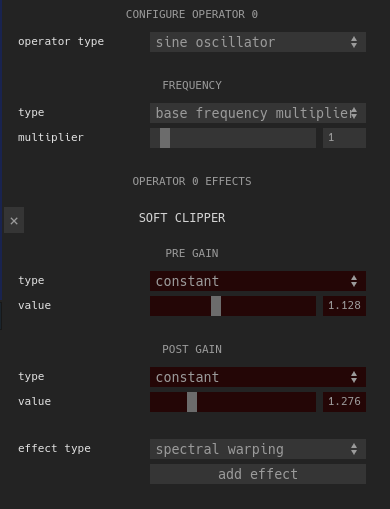
There are controls for how the frequency of the operator is determined which defaults to base frequency multiplier. This means that the frequency of whatever note the oscillator is playing (after applying [detune]) is multiplied by the selected base frequency multiplier and is then used as the frequency of that operator. In FM synthesis, the values that sound best are usually fairly regular multiples of the base frequency like 1, 4, 2, 0.5, etc. Using base frequency multipliers like 2.125 or non-base-frequency-multiplies such as constant frequencies in hertz or outputs from an [envelope-generator] often results in dissonant sounds or noise being generated.

modulation index configuration

The [modulation-index] of each operator->operator pair can be set by either clicking on the square in question and using the UI shown to the right, or by scrolling with the mouse scroll wheel while hovering over the square.

Both positive and negative modulation indices are supported, but they function largely the same except for cases where feedback is involved.

feedback

Feedback occurs in the modulation matrix if any of the squares along the x=y diagonal are non-zero or if any loop occurs in the graph. For example, this is what an [operator] modulating itself directly via feedback looks like:

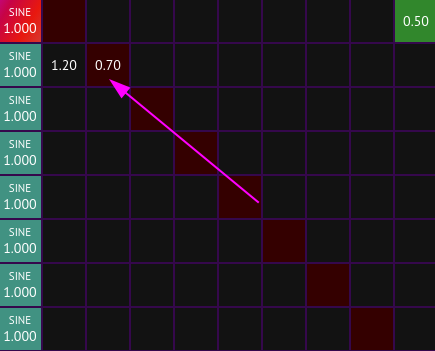
And this is an example of a loop in the modulation matrix where operator 2 modulates operator 1 which in turn modules operator 2, creating a feedback loop:

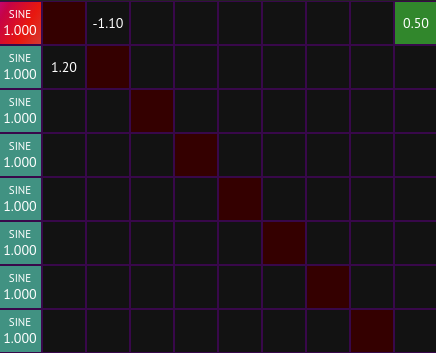
It is important to be careful when using feedback; it is very easy for the modulation matrix to become unstable if feedback exists with high modulation indices. I've found that keeping modulation indices below 1 for direct feedback and below ~1.5 for feedback loops with multiple operators is a good idea.